一道Shor算法的例题
试试看用Shor算法分解一个比较大的数\(N\)。具体方法Nielson的那本书写的很清楚。
真正试过才知道为什么例题总是给\(N=15\)这样小的数,数字大了经典计算机根本解不动\(r\text{ s.t. }x^r\equiv1\pmod{N}\);QFT分解部分,数字大了经典计算机也算不动。
以\(N=113\times127=14\ 351\)为例,(这个数我凑了好久),在计算\(r\text{ s.t. }x^r\equiv1\pmod{N}\)时比较好算。
该问题的部分解
对于 $$r\text{ s.t. }x^r\equiv1\pmod{14\ 351}$$ 有解: $$\begin{align} x=2,r=28\\\ x=2,r=56\\\ x=2,r=84\\\ x=4,r=14\\\ x=4,r=42\\\ x=4,r=70\\\ x=16,r=21\\\ x=16,r=35\\\ x=16,r=49 \end{align}$$随便挑一个数\(x=2\)。
将\(N\)转换成二进制。
$$ (14\ 351)_{10}=(11\ 100\ 000\ 001\ 111)_2 $$
一共是14比特,如果希望最终结果错误率\(\epsilon\le1\%\),则至少需要35个\(\ket{0}\)。还至少需要14个qubit来储存\(\ket{2^j\bmod14\ 351}\)的结果。
下面开始计算:
-
初始状态为\(\ket{0}^{\otimes35}\ket{1}^{\otimes14}\);
-
35个Hadamard门作用在\(\ket{0}^{\otimes35}\)上,将其变换为\(\frac{1}{\sqrt{2^{35}}}\sum_{j=0}^{2^{35}-1}\ket{j}\ket{1}^{\otimes14}\);
-
通过黑匣子将状态变为\(\frac{1}{\sqrt{2^{35}}}\sum_{j=0}^{2^{35}-1}\ket{j}\ket{2^j\bmod14\ 351}\)
-
对后14个qubit作QFT量子傅立叶变换,前35个qubit的状态变为\(\sum_ya_y\ket{y}\),相对概率画出来是这样的:
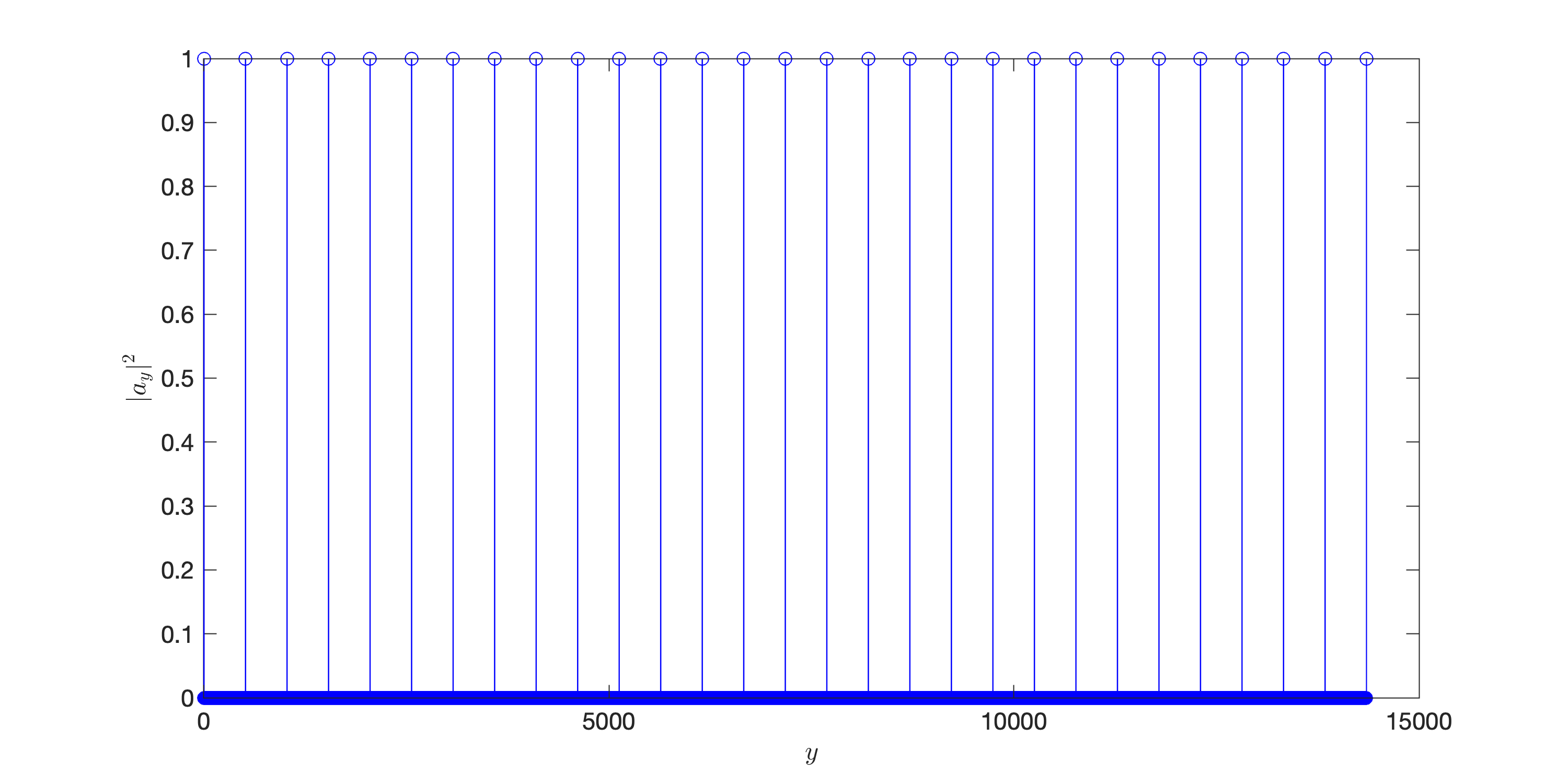
- 测量前35个qubit后,将随机得到一个数,假设测得13 843,作连分式展开: $$ \frac{13\ 843}{2^{35}}=0+\frac{1}{2\ 482\ 102+\frac{1}{36+\frac{1}{4+\frac{1}{5+\frac{1}{18}}}}} $$
写成5阶渐进分数的形式为\(\frac{13\ 843}{2^{35}}=[0, 2\ 482\ 102, 36, 4, 5, 18]\)
Mathematica有现成的代码。
|
|
一阶近似: $$ \frac{13\ 843}{2^{35}}\approx0+\frac{1}{2\ 482\ 102}=\frac{1}{2\ 482\ 102} $$
尝试一下\(r=2\ 482\ 102\): $$ 2^{r/2}\bmod14\ 351=128 $$
因此\(r=2\ 482\ 102\)是我们想要的一个解。
- 计算\(\text{gcd}(x^{r/2}-1,N)\)和\(\text{gcd}(x^{r/2}+1,N)\): $$\begin{align} \text{gcd}(x^{r/2}-1,N)=127\\ \text{gcd}(x^{r/2}+1,N)=1 \end{align}$$
得到\(N=14\ 351\)的一个因数\(127\),很容易就能得到另一个因数\(113\)。